Discussion 5: Tree Recursion

• disc05.pdf

If there are fewer than 3 people in your group, feel free to merge your group with another group in the room.

Now switch to Pensieve:

• Everyone: Go to pensieve.co, log in with your @berkeley.edu email, and enter your group number (which was in the email that assigned you to this lab).

Once you're on Pensieve, you don't need to return to this page; Pensieve has all the same content (but more features). If for some reason Penseive doesn't work, return to this page and continue with the discussion.

Getting Started

Everyone say your name and one tip for what to do when the weather gets hot.

[For Fun] This emoticon of a guy in a cowboy hat is valid Python: o[:-D]

>>> o = [2, 0, 2, 4]
>>> [ o[:-D] for D in range(1,4) ]
[[2, 0, 2], [2, 0], [2]]

🤠

Tree Recursion

For the following questions, don't start trying to write code right away. Instead, start by describing the recursive case in words. Some examples:

• In fib from lecture, the recursive case is to add together the previous two Fibonacci numbers.
• In double_eights from lab, the recursive case is to check for double eights in the rest of the number.
• In count_partitions from lecture, the recursive case is to partition n-m using parts up to size m and to partition n using parts up to size m-1.

Q1: Insect Combinatorics

An insect is inside an m by n grid. The insect starts at the bottom-left corner (1, 1) and wants to end up at the top-right corner (m, n). The insect can only move up or to the right. Write a function paths that takes the height and width of a grid and returns the number of paths the insect can take from the start to the end. (There is a closed-form solution to this problem, but try to answer it with recursion.)

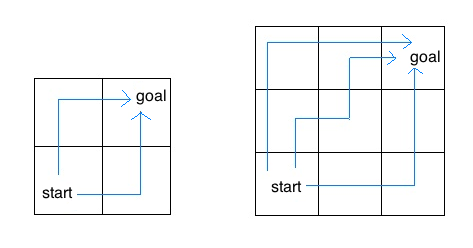
In the 2 by 2 grid, the insect has two paths from the start to the end. In the 3 by 3 grid, the insect has six paths (only three are shown above).

Hint: What happens if the insect hits the upper or rightmost edge of the grid?

Run in 61A Code

Tree Recursion with Lists

[New] Some of you already know list operations that we haven't covered yet, such as append. Don't use those today. All you need are list literals (e.g., [1, 2, 3]), item selection (e.g., s[0]), list addition (e.g., [1] + [2, 3]), len (e.g., len(s)), and slicing (e.g., s[1:]). Use those! There will be plenty of time for other list operations when we introduce them next week.

The most important thing to remember about lists is that a non-empty list s can be split into its first element s[0] and the rest of the list s[1:].

>>> s = [2, 3, 6, 4]
>>> s[0]
2
>>> s[1:]
[3, 6, 4]

Q2: Max Product

Implement max_product, which takes a list of numbers and returns the maximum product that can be formed by multiplying together non-consecutive elements of the list. Assume that all numbers in the input list are greater than or equal to 1.

Run in 61A Code Hint More Help

New Rule: Whoever in your group typed the answer to the last question should not type the answer to the next one. Instead, just ask questions and give suggestions; give other members of your group a chance to type the answer.

Q3: Sum Fun

Implement sums(n, m), which takes a total n and maximum m. It returns a list of all lists:

1. that sum to n,
2. that contain only positive numbers up to m, and
3. in which no two adjacent numbers are the same.

Two lists with the same numbers in a different order should both be returned.

Here's a recursive approach that matches the template below: build up the result list by building all lists that sum to n and start with k, for each k from 1 to m. For example, the result of sums(5, 3) is made up of three lists:

• [[1, 3, 1]] starts with 1,
• [[2, 1, 2], [2, 3]] start with 2, and
• [[3, 2]] starts with 3.

Hint: Use [k] + s for a number k and list s to build a list that starts with k and then has all the elements of s.

>>> k = 2
>>> s = [4, 3, 1]
>>> [k] + s
[2, 4, 3, 1]

Run in 61A Code Hint: First Blank Hint: Second Blank Hint: Third Blank

If you get stuck (which many groups do), ask for help!

Document the Occasion

Please all fill out the attendance form (one submission per person per week).