Lab 5 Solutions
Solution Files
Topics
Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the questions and refer back here should you get stuck.
Tree Recursion
A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.
For example, this is the Virahanka-Fibonacci sequence:
0, 1, 1, 2, 3, 5, 8, 13, ....
Each term is the sum of the previous two terms. This tree-recursive function calculates the nth Virahanka-Fibonacci number.
def virfib(n):
if n == 0 or n == 1:
return n
return virfib(n - 1) + virfib(n - 2)Calling virfib(6) results in a call structure that resembles
an upside-down tree (where f is virfib):

Each recursive call f(i) makes a call to f(i-1) and a call to f(i-2).
Whenever we reach an f(0) or f(1) call, we can directly return 0 or 1
without making more recursive calls. These calls are our base cases.
A base case returns an answer without depending on the results of other calls. Once we reach a base case, we can go back and answer the recursive calls that led to the base case.
As we will see, tree recursion is often effective for problems with branching choices. In these problems, you make a recursive call for each branching choice.
Examples
Here are some examples of tree-recursive problems:
- Given a list of paid tasks and a limited amount of time, which tasks should you choose to maximize your pay? This is actually a variation of the Knapsack problem, which focuses on finding some optimal combination of items.
- Suppose you are lost in a maze and see several different paths. How do you find your way out? This is an example of path finding, and is tree recursive because at every step, you could have multiple directions to choose from that could lead out of the maze.
- Your dryer costs $2 per cycle and accepts all types of coins. How many different combinations of coins can you create to run the dryer? This is similar to the partitions problem from the textbook.
Required Questions
Q1: Fibonacci
Write the fibonacci function using tree recursion.
The function should take in n and return the nth
fibonacci number.
As a reminder, Fibonacci is defined as a function where:
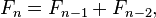
def fibonacci(n):
"""Return the nth fibonacci number.
>>> fibonacci(11)
89
>>> fibonacci(5)
5
>>> fibonacci(0)
0
>>> fibonacci(1)
1
"""
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)Use Ok to test your code:
python3 ok -q fibonacciQ2: Insect Combinatorics
Consider an insect in an M by N grid. The insect starts at the
bottom left corner, (1, 1), and wants to end up at the top right
corner, (M, N). The insect is only capable of moving right or
up. Write a function paths that takes a grid length and width
and returns the number of different paths the insect can take from the
start to the goal. (There is a closed-form solution to this problem,
but try to answer it procedurally using recursion.)

For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).
Hint: What happens if we hit the top or rightmost edge?
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
if m == 1 or n == 1:
return 1
return paths(m - 1, n) + paths(m, n - 1)
# Base case: Look at the two visual examples given. Since the insect
# can only move to the right or up, once it hits either the rightmost edge
# or the upper edge, it has a single remaining path -- the insect has
# no choice but to go straight up or straight right (respectively) at that point.
# There is no way for it to backtrack by going left or down.Use Ok to test your code:
python3 ok -q pathsQ3: Partition
The number of partitions of a positive integer n is the number of
ways in which n can be expressed as the sum of positive integers in
increasing order. For example, the number 5 has 7 partitions.
5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 1 + 1 + 1Write a tree-recursive function partition(n) that returns the number of
partitions of n.
Hint: Introduce a helper function that computes partitions of n using
only a subset of the integers less than or equal to n. Once you have
done so, you can use very similar logic to the count_change function
from the lecture notes:
def partition(n):
"""Return the number of partitions of positive integer n.
>>> partition(5)
7
>>> partition(10)
42
>>> partition(15)
176
>>> partition(20)
627
"""
return part_max(n, n)
def part_max(n, m):
"""Return the number of partitions of n using integers up to m.
>>> part_max(5, 3)
5
"""
if n < 0 or m <= 0:
return 0
if n == 0:
return 1
return part_max(n-m, m) + part_max(n, m-1)Use Ok to test your code:
python3 ok -q partitionCheck Your Score Locally
You can locally check your score on each question of this assignment by running
python3 ok --scoreThis does NOT submit the assignment! When you are satisfied with your score, submit the assignment to Gradescope to receive credit for it.
Submit Assignment
Submit this assignment by uploading any files you've edited to the appropriate Gradescope assignment. Lab 00 has detailed instructions.