Homework 1
Due at 11:59:59 pm on 02/01/2024.

Instructions

Download hw01.zip. Inside the archive, you will find starter files for the questions in this homework, along with a copy of the OK autograder.

Readings: This homework relies on following references:

• Section 1.2
• Section 1.3
• Section 1.5

Review from lab

Division

Let's compare the different division-related operators in Python:

>>> 1 / 5
0.2

>>> 25 / 4
6.25

>>> 5 / 0
ZeroDivisionError

>>> 1 // 5
0

>>> 25 // 4
6

>>> 5 // 0
ZeroDivisionError

>>> 1 % 5
1

>>> 25 % 4
1

>>> 5 % 0
ZeroDivisionError

Note that floor division and modulo both return an integer while true division always returns a floating point number.
For now, the only difference you need to understand between integers and floats is that integers are positive or negative whole numbers, while floats are positive or negative decimals.

One useful technique involving the % operator is to check whether a number x is divisible by another number y:

x % y == 0

For example, in order to check if x is an even number:

x % 2 == 0

Floats and precedence

Floating point numbers (floats) behave a lot like real numbers. You can identify a float by the decimal point. All floats have decimal points. To write a floating point number (as a literal), you must add a decimal point!

>>> 3.141592
3.141592
>>> 2 * 3.141592  # you can mix ints and floats 
6.283184
>>> pie = 3.141592  # you can assign values to variables
>>> pie
3.141592
>>> pie / pie
1.0
>>> pie / pie == 1  # a float can be equal in value to an int
True
>>> from math import pi  # here is a better pi
>>> pi
3.141592653589793
>>> 5.0 / 3.0  # this is division of floats, not ints
1.6666666666666667
>>> 2 ** (1 / 2) # square root - isn't that transcendental?
1.4142135623730951

Expressions follow operator precedence (just like in math). Operations are performed one at a time in a specific order. Parenthesis are used to specify order (again, just like in math - remember PEMDAS?).

>>> 2 + 3 - 4 + 5   # equal precedence, left to right
6
>>> 2 + 3 - (4 + 5) # order matters - parentheses are your friend
-4
>>> (((2 + 3) - 4) + 5) # explicit order of the first example
6
>>> 2 + 3 * 4   # * and / bind more tightly than + or - 
14
>>> 2 + (3 * 4) 
14
>>> (2 + 3) * 4  
20
>>> 2 + 3 / 4 * 5  # what about * and / ?
5.75

An expression can have multiple return values, called a tuple:

>>> 2, 3
(2, 3)
>>> x, y = 1, pi
>>> x
1
>>> y
3.141592653589793

Strings

It is very useful to be able to write programs that operate on strings, not just numbers. Without strings, web browsers and word processors would be like the matrix! Just as with ints, floats, and booleans, strings are a data type and have certain operators defined on them:

>>> 'cal'           # a string literal is a sequence of characters in quotes
'cal'
>>> "rocks"         # either kind of quote, but they need to match
'rocks'
>>> "cal" + "rocks"   # + is concatenation
'calrocks'
>>> 'cal' * 3         # * is replication
'calcalcal'
>>> 'cal' == "cal"  # equality is if they are the same string (notice the single and double quotes)
True
>>> 'Cal' == 'cal'  # case sensitive
False
>>> 'Cal' < 'cal'   # lexicographic ordering, with upper before lower case
True
>>> 'you' is not 'me'
True

Problems

Question 1: Oddly we go

Define odd, which takes an integer and returns whether it is odd. Your solution will look like return <expression>.

 def odd(number):
     """Return whether the number is odd.

     >>> odd(2)
     False
     >>> odd(5)
     True
     """
     "*** YOUR CODE HERE ***"

Use OK to test your code:

python3 ok -q odd

Question 2: Distance

Implement a function called distance(x1, y1, x2, y2) where:

• x1 and y1 form an x-y coordinate pair
• x2 and y2 form an x-y coordinate pair

distance returns the Euclidean distance between the two points. Use the following formula:

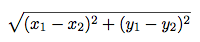
from math import sqrt

def distance(x1, y1, x2, y2):
    """Calculates the Euclidian distance between two points (x1, y1) and (x2, y2)

    >>> distance(1, 1, 1, 2)
    1.0
    >>> distance(1, 3, 1, 1)
    2.0
    >>> distance(1, 2, 3, 4)
    2.8284271247461903
    """
    "*** YOUR CODE HERE ***"

Use OK to test your code:

python3 ok -q distance

Question 3: Distance (3-D)

Now, let us edit this program to get the distance between two 3-dimensional coordinates. Your distance3d function should take six arguments and compute the following:

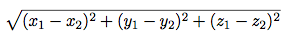
def distance3d(x1, y1, z1, x2, y2, z2):
    """Calculates the 3D Euclidian distance between two points (x1, y1, z1) and
    (x2, y2, z2).

    >>> distance3d(1, 1, 1, 1, 2, 1)
    1.0
    >>> distance3d(2, 3, 5, 5, 8, 3)
    6.164414002968976
    """
    "*** YOUR CODE HERE ***"

Use OK to test your code:

python3 ok -q distance3d

Question 4: Add absolute

Implement the function a_plus_abs_b which takes 2 numbers a and b, and returns the result of doing a plus the absolute value of b. You must not modify the template in the starter code, use the abs function, or define any new functions - you can only fill in the blanks.

Hint: We've seen that we can name a value by assigning it to a variable. Functions are values too. Try typing the name of a function you have defined or imported into the python interpreter, and then assigning it to a variable, e.g.:

>>> from operator import add
>>> my_func = add
>>> my_func(5, 10) == add(5, 10)
True
>>> type(my_func)
<class 'builtin_function_or_method'>
>> type(add)
<class 'builtin_function_or_method'>

How can you use the imported functions to solve this problem?

from operator import add, sub

def a_plus_abs_b(a, b):
    """Return a+abs(b), but without calling abs.

    >>> a_plus_abs_b(2, 3)
    5
    >>> a_plus_abs_b(2, -3)
    5
    >>> a_plus_abs_b(-5, -1)
    -4
    """
    if b < 0:
        f = _____
    else:
        f = _____
    return f(a, b) # You can replace this line, but don't have to.

Use OK to test your code:

python3 ok -q a_plus_abs_b

Question 5: Quadratic Formula

Complete the function so that it returns a tuple that contains both roots of a quadratic polynomial using the quadratic formula. The first element in the tuple should be the "plus" case and the second element should be the "minus" case. Your solution must call the sqrt function exactly once.

See here for a basic tuple example.

from math import sqrt

def quadratic(a, b, c):
    """
    >>> quadratic(1, 0, -1)
    (1.0, -1.0)
    >>> quadratic(1, 2, 1)
    (-1.0, -1.0)
    >>> quadratic(1, 3, -4)
    (1.0, -4.0)
    """
    "*** YOUR CODE HERE ***"

Use OK to test your code:

python3 ok -q quadratic

Question 6: Falling Factorial

Let's write a function falling, which is a "falling" factorial that takes two arguments, n and k, and returns the product of k consecutive numbers, starting from n and working downwards.

If k is larger than n, only multiply up to n consecutive numbers!

def falling(n, k):
    """Compute the falling factorial of n to depth k.

    >>> falling(6, 3)  # 6 * 5 * 4
    120
    >>> falling(4, 3)  # 4 * 3 * 2
    24
    >>> falling(4, 1)  # 4
    4
    >>> falling(4, 0)
    1
    """
    "*** YOUR CODE HERE ***"

Use OK to test your code:

python3 ok -q falling

Question 7: Hailstone

Complete this question using iteration!

Douglas Hofstadter's Pulitzer-prize-winning book, Gödel, Escher, Bach, poses the following mathematical puzzle:

1. Pick a positive integer n as the start.
2. If n is even, divide it by 2.
3. If n is odd, multiply it by 3 and add 1.
4. Continue this process until n is 1.

The sequence of values of n is often called a Hailstone sequence, because hailstones also travel up and down in the atmosphere before falling to earth. Write a function that takes a single argument with formal parameter name n, prints out the hailstone sequence starting at n, and returns the number of steps in the sequence:

Note: Use floor division (can you think of why?)

def hailstone(n):
    """Print the hailstone sequence starting at n and return its
    length.

    >>> a = hailstone(2)
    2
    1
    >>> a
    2
    >>> b = hailstone(10)
    10
    5
    16
    8
    4
    2
    1
    >>> b
    7
    """
    "*** YOUR CODE HERE ***"

Hailstone sequences can get quite long! Try 27. What's the longest you can find?

Use OK to test your code:

python3 ok -q hailstone

Optional Questions

Question 8: Harmonic Mean

Implement harmonic_mean, which returns the harmonic mean of two positive numbers x and y. The harmonic mean of 2 numbers is 2 divided by the sum of the reciprocals of the numbers. (The reciprocal of x is 1/x.)

def harmonic_mean(x, y):
    """Return the harmonic mean of x and y.

    >>> harmonic_mean(2, 6)
    3.0
    >>> harmonic_mean(1, 1)
    1.0
    >>> harmonic_mean(2.5, 7.5)
    3.75
    >>> harmonic_mean(4, 12)
    6.0
    """
    "*** YOUR CODE HERE ***"

Use OK to test your code:

python3 ok -q harmonic_mean

Question 9: Two of three

Write a function that takes three positive numbers and returns the sum of the squares of the two largest numbers. Use only a single expression for the body of the function.

def two_of_three(a, b, c):
    """Return x * x + y * y, where x and y are the two largest members of the
    positive numbers a, b, and c.

    >>> two_of_three(1, 2, 3)
    13
    >>> two_of_three(5, 3, 1)
    34
    >>> two_of_three(10, 2, 8)
    164
    >>> two_of_three(5, 5, 5)
    50
    """
    "*** YOUR CODE HERE ***"

Use OK to test your code:

python3 ok -q two_of_three

Submission

When you are done, submit your file to Gradescope. You only need to upload the following files:

• hw01.py